Výpočet povrchu vrchlíku rotačního elipsoidu
14 Jun 2010
Výpočet povrchu vrchlíku elipsoidu není tak triviální, jako výpočet povrchu vrchlíku koule. Proto muselo být učiněno několik zjednodušení. Následující odvození funguje jen pro rotační elipsoid, který je zploštělý v ose rotace.
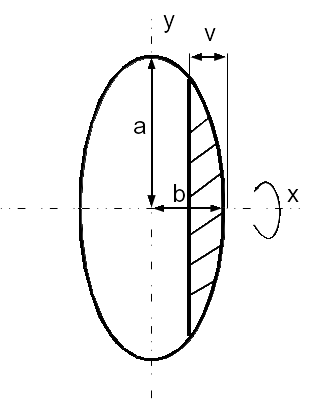
Postup odvození
Nejprve potřebuji funkci křivky pro část elipsy, kterou budu rotovat.
Používám elipsu umístěnou ve středu souřadnicového systému. Rotuje se
podle osy x. V ose y je poloosa a a
v ose x je poloosa b. Pro odvození postačí funkce
na intervalu x>=0 a y>=0. Dále je pak
definován vztah poloos elipsy kde platí že a>b (zploštělá
elipsa).
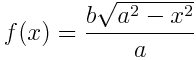
Pro výpočet povrchu je třeba definovat interval na ose y, ale
já potřebuji interval na ose x, musím tedy provést přepočet.
Integrál budu počítat od 0 do alfa, kde alfa je
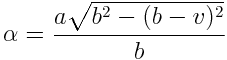
Vztah pro výpočet povrchu vrchlíku tedy je
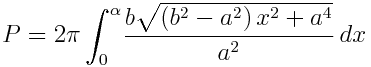
A po integraci a dosazení alfa vyjde vztah
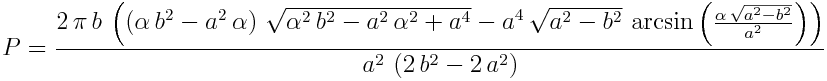
Vztah je poměrně komplikovaný, takže pokud bych chtěl podle něj
počítat, trochu si ho zjednoduším. Vyjádřím si různé části vedle,
které se pak budu snažit ve vzorci nahradit. Tímto vznikly vztahy pro
výpočet E, F, G
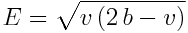
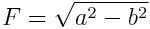
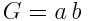
A následná konečná podoba vzorce pro výpočet vrchlíku je
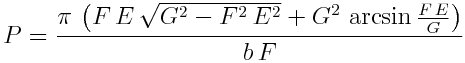
Vzhledem k postupu odvození funguje vztah pouze pro v<=b.
Výpočet v programu Matlab pak může být následující
function [S] = plocha_vrchliku(a,b,v)
% plocha vrchliku rotacniho elipsoidu
% musi platit a>0, b>0, a>b, b>=v
E = sqrt(v.*(2*b-v));
F = sqrt(a^2-b^2);
G = a*b;
S = pi*(F*E.*sqrt(G^2 - F^2*E.^2)+G^2*asin(F*E/G))/(b*F);
Závěr
Použitý vzorec je funkční a lze jím spočítat povrch vrchlíku rotačního elipsoidu, je třeba ale dbát na to, aby se výpočet neprováděl mimo definované meze, kde již nefunguje.
Použitá literatura
- [1] Jan Končel, Analytická geometrie – Kuželosečky – Elipsa, 2009
- [2] Eva Schlesingerová, Integrílní počet – Povrch pláště rotačního tělesa
